Welch Two Sample t-test
data: imd_decile by factor(blood_pressure)
t = 0.00075095, df = 38.97, p-value = 0.9994
alternative hypothesis: true difference in means between group high bp and group normal is not equal to 0
95 percent confidence interval:
-0.7869881 0.7875726
sample estimates:
mean in group high bp mean in group normal
4.538462 4.538169 R 4: Data Analysis
Learning objectives
Perform tests of difference such as t-test and ANOVA
Perform linear regression
Pick a dataset to clean, explore, and analyse!
Our project for this worksheet is to run some analysis on the data we have been cleaning and visualising! By the end of the worksheet you will have performed a t-test, ANOVA, and multiple linear regression on the dataset.
You will also be given the opportunity to explore one of the example datasets provided, with a trainer on hand to help if needed.
Setup
- This time you will be opening your own R script or R Markdown file. First, make sure you are in the RStudio project we setup in the data cleaning worksheet. Then follow the instructions below.
To open a script you can either go to
File > New File > R Scriptor use the keyboard shortcutshift + command/control + N.To open a new R markdown file go to
File > New File > R Markdown. When opening we recommend you change the title toR_4. Then when the file is open we suggest deleting everything after line 6 or under the second---. You’ll need to add your own headings using the#and add code cells usingoption+command+ion a Mac orctrl + alt + ion a Windows machine.
Install the
broom,easystats, andstargazerlibraries which we will be using for reporting. We recommend installing packages using the command line as you only need to install packages once.Load tidyverse, easystats, broom, and stargazer.
Load in the heath metrics dataset. You should already have it, but if you can’t find it we have provided a download of it below.
Recommended resources
Throughout this session we will be working with statistics but explaining these statistical tests is beyond the scope of this workshop. As such here are some recommended resources around statistical help.
LSE Life Quant advisers offer 1-2-1 support around quantitative methods.
Statquest is a YouTube channel that provides clear explanations of statistical methods, and how do do them in R.
Take this example of how to do a linear regression in R
Or this for a multiple linear regression in R
Modern stats with R book provides some useful examples
R tutor which provides short examples of lots of statistical tests.
R statistics tutorials which are longer tutorials on models like regression.
Exploring tests of difference: t-test and ANOVA
Tests of difference such as t-tests and ANOVAs are designed to statistically measure the differences between groups or samples. These tests are usually based around a comparison between average values.
There are many versions of these tests and it is beyond the scope of this workshop to cover those. Instead we will pick one or two which match our data, and figure out how to run these tests in R!
The reason we run statistical tests is that we have questions we want to answer. In science we call this hypothesis testing. We form a question via a hypothesis, then we use a statistical test to help answer it. See this article for a quick intro to creating a hypothesis.
t-test
A t-test is used to compare the means of two groups. We have two questions we want to answer where a t-test is a good test to use.
Question 1: is there a statistical difference of average index of multiple deprivation (IMD) decile between those who have high or normal blood pressure?
You should end up with a result like the output below.
Factors are important when it comes to running statistical tests using R. To compare by groups you might need to convert your grouping variable (i.e. blood pressure) to a factor using factor().
The output gives you lots of useful information. To know if there is a statistical difference you need to look at the t and the p-value. Generally a t over 2-2.5 will give you a significant difference, and you are looking for a p-value under 0.05.
Question 2: is there a statistical difference in IMD decile between people who are from Hackney and Westminster?
You should end up with a result like the output below.
Welch Two Sample t-test
data: hackney$imd_decile and westminster$imd_decile
t = -19.481, df = 496.41, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-3.048357 -2.489812
sample estimates:
mean of x mean of y
2.818681 5.587766 You will need to create a data frame for people who are from Hackney and people who are from Westminster.
A p-value of 2.2e-16 represents a very small value in scientific notation. In decimal form, it is equivalent to 0.00000000000000022.
ANOVA
Analysis of variance (ANOVA) is a statistical test (or set of statistical models) used to compare the difference between means of groups.
In our previous t-test we wanted to know if there was a difference average IMD decile between people from Hackney and Westminster. What if we wanted to know if there is a statistical difference across all locations? We can use an ANOVA to test this difference!
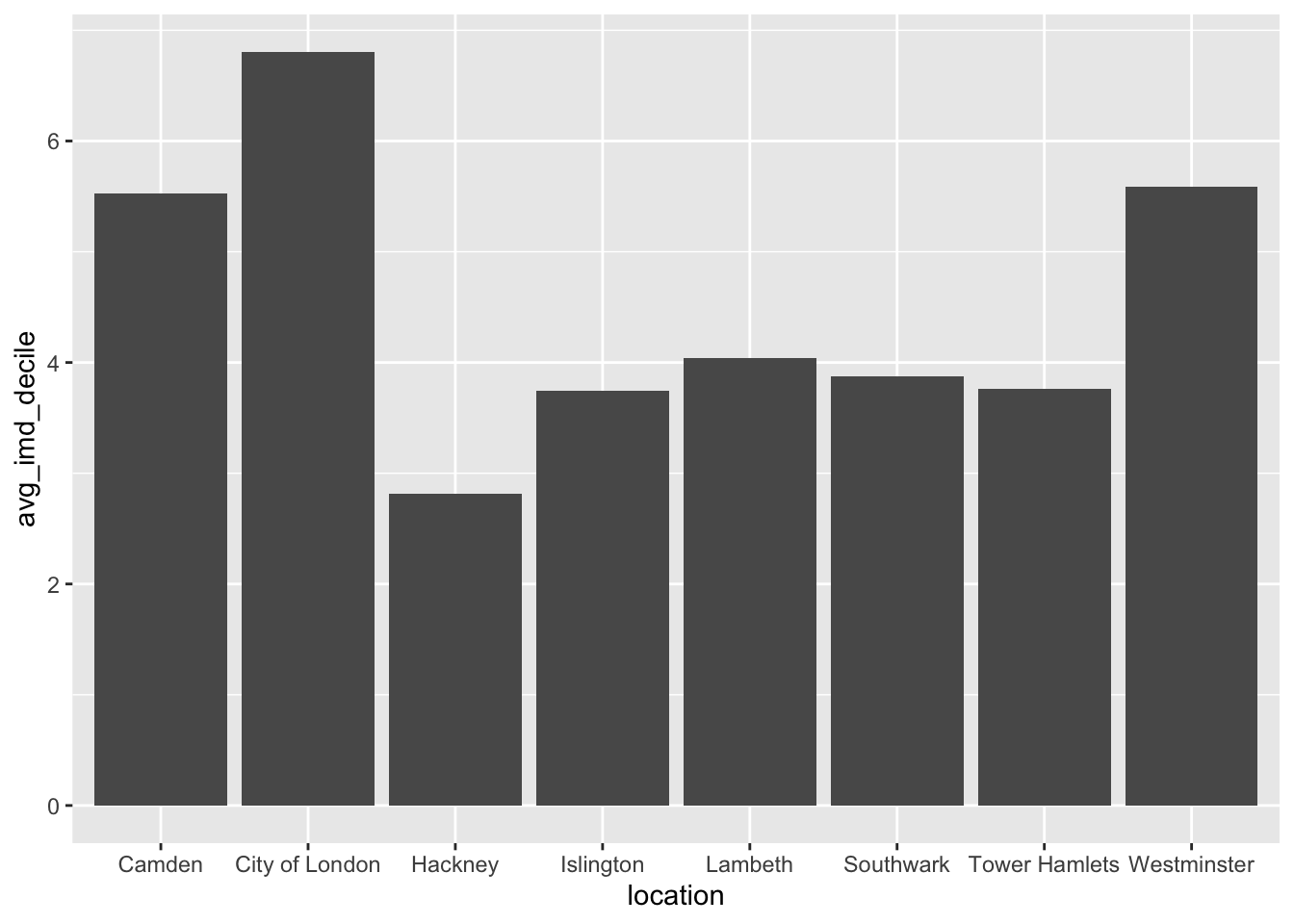
We have looked at the difference between these groups previously. Have a look at the visual below. Do you think we might see a statistical difference between locations and the average IMD decile?
Our question we want to answer: is there a difference in average IMD decile between London Boroughs?
You should end up with results like the outputs below.
Df Sum Sq Mean Sq F value Pr(>F)
location 7 4432 633.1 158.4 <2e-16 ***
Residuals 2926 11693 4.0
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = imd_decile ~ location, data = health)
$location
diff lwr upr p adj
City of London-Camden 1.28133560 0.8386821 1.7239891 0.0000000
Hackney-Camden -2.70599401 -3.1492705 -2.2627175 0.0000000
Islington-Camden -1.77952297 -2.2237452 -1.3353007 0.0000000
Lambeth-Camden -1.48300866 -1.9203113 -1.0457060 0.0000000
Southwark-Camden -1.64712430 -2.0973219 -1.1969267 0.0000000
Tower Hamlets-Camden -1.76129504 -2.2074505 -1.3151396 0.0000000
Westminster-Camden 0.06309063 -0.3765349 0.5027162 0.9998668
Hackney-City of London -3.98732961 -4.4361629 -3.5384963 0.0000000
Islington-City of London -3.06085857 -3.5106259 -2.6110912 0.0000000
Lambeth-City of London -2.76434426 -3.2072786 -2.3214099 0.0000000
Southwark-City of London -2.92845991 -3.3841299 -2.4727900 0.0000000
Tower Hamlets-City of London -3.04263065 -3.4943075 -2.5909538 0.0000000
Westminster-City of London -1.21824497 -1.6634729 -0.7730171 0.0000000
Islington-Hackney 0.92647104 0.4760905 1.3768515 0.0000000
Lambeth-Hackney 1.22298535 0.7794284 1.6665423 0.0000000
Southwark-Hackney 1.05886970 0.6025945 1.5151449 0.0000000
Tower Hamlets-Hackney 0.94469896 0.4924116 1.3969863 0.0000000
Westminster-Hackney 2.76908464 2.3232374 3.2149319 0.0000000
Lambeth-Islington 0.29651431 -0.1479878 0.7410164 0.4661226
Southwark-Islington 0.13239867 -0.3247954 0.5895927 0.9879815
Tower Hamlets-Islington 0.01822793 -0.4349864 0.4714422 1.0000000
Westminster-Islington 1.84261360 1.3958260 2.2894012 0.0000000
Southwark-Lambeth -0.16411565 -0.6145893 0.2863580 0.9559037
Tower Hamlets-Lambeth -0.27828638 -0.7247204 0.1681477 0.5574446
Westminster-Lambeth 1.54609929 1.1061910 1.9860076 0.0000000
Tower Hamlets-Southwark -0.11417074 -0.5732433 0.3449018 0.9952301
Westminster-Southwark 1.71021494 1.2574859 2.1629440 0.0000000
Westminster-Tower Hamlets 1.82438568 1.3756760 2.2730954 0.0000000Location needs to be made a factor for the test to run.
We used the following functions: aov(), summary(), and TukeyHSD().
The test we have done here is called a one-way ANOVA. The key statistics we look for in an ANOVA test are the F value and the Pr(>F).
The higher the F-value in an ANOVA, the higher the variation between sample means relative to the variation within the samples. The higher the F-value, the lower the corresponding p-value.
The Tukey multiple comparisons of means shows us all the different comparisons and which were or were not significantly different.
Regression
A regression can come in many forms. The most common is the ordinary least squares regression (OLS) which is also known as a linear regression. It is called linear because a straight line is used to estimate the relationship between two variables. In statistics regressions are used to estimate the relationship between a dependent variable and one or more independent variables.
As building regression models is similar across different models in R we will focus on linear regression. The key take ways are:
Basic code and formula building which is similar across all regression functions in R.
How to interpret the output.
Building multiple linear regressions (as in using multiple independent variables).
How are dummy variables used.
Side note on dummy variables
Dummy variables are artificial variables that take values of 0 or 1 to indicate the absence or presence of something.
0 = absent
1 = present
By convention if you have two or more variables, one variable is not coded so we have a comparison point (also known as a reference).
For example, if we give people a choice of three ice cream flavours and they tell us their favourite (Vanilla, Chocolate, or Pistachio), we would use two dummy variables. In the table below we have used vanilla as our comparison point with dummy variables for pistachio and chocolate.
| Favourite_ice_cream | dummy_pistachio | dummy_chocolate |
|---|---|---|
| Vanilla | 0 | 0 |
| Chocolate | 0 | 1 |
| Pistachio | 1 | 0 |
| Vanilla | 0 | 0 |
| Vanilla | 0 | 0 |
| Chocolate | 0 | 1 |
When you look your regression output you will see all the different categories apart from your comparison/reference variable.
You do not need to create dummy variables in R, this is handled automatically using factors. There is a useful explanation of dummy variables in this book.
An important thing to note about using factors as dummy variables is the first level in that factor will be used as your reference. To change this you need to change the order of your factor levels.
Building regression models
Our question is around the IMD decile. We want to know what the relationship is with the IMD decile with other variables in our dataset. As IMD decile is our focus this will be our dependent variable.
Model 1: Simple linear regression
For our first model we are wanting to know the relationship between our dependent variable IMD decile and an independent variable of waist to hip ratio (whr).
You should end up with result like the output below.
Call:
lm(formula = imd_decile ~ whr, data = health)
Residuals:
Min 1Q Median 3Q Max
-3.6298 -1.5692 -0.5455 1.4632 5.6012
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.0547 0.5160 9.795 <2e-16 ***
whr -0.6109 0.6082 -1.004 0.315
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.345 on 2932 degrees of freedom
Multiple R-squared: 0.000344, Adjusted R-squared: 3.041e-06
F-statistic: 1.009 on 1 and 2932 DF, p-value: 0.3152Model 2: Multiple linear regression
For our second model we are wanting to know the relationship between our dependent variable IMD decile, imd_decile, and an independent variables of location, BMI, waist to hip ratio, and age.
You should end up with result like the output below.
Call:
lm(formula = imd_decile ~ location + bmi + whr + age, data = health)
Residuals:
Min 1Q Median 3Q Max
-4.6673 -1.5906 -0.0768 1.2854 6.2056
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.387032 0.488719 15.115 <2e-16 ***
locationCamden -1.286067 0.146982 -8.750 <2e-16 ***
locationHackney -4.007404 0.148922 -26.909 <2e-16 ***
locationIslington -3.090634 0.149319 -20.698 <2e-16 ***
locationLambeth -2.777376 0.146672 -18.936 <2e-16 ***
locationSouthwark -2.925688 0.150988 -19.377 <2e-16 ***
locationTower Hamlets -3.052334 0.149878 -20.366 <2e-16 ***
locationWestminster -1.226694 0.147252 -8.331 <2e-16 ***
bmi 0.001591 0.006465 0.246 0.806
whr -0.822813 0.522622 -1.574 0.116
age 0.001784 0.002019 0.884 0.377
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.003 on 2896 degrees of freedom
(27 observations deleted due to missingness)
Multiple R-squared: 0.2767, Adjusted R-squared: 0.2742
F-statistic: 110.8 on 10 and 2896 DF, p-value: < 2.2e-16For our model we moved our dummy variable reference to City of London by changing the order of the factor levels. This is because City of London has the highest IMD decile average.
The lm() function is the simplest way to run OLS models in R.
If you want to just look at the coefficients of the model we can use the coefficients() function. If we wanted to use a different modelling family to OLS we would use the glm() function and specify which model family to use such as binomial which is a logit model. Across R the way of building models is very similar to using the lm() function.
Writing your results in a publication ready format
We have done some analysis which is great, but we can also use R to get our results in a format to put into reports.
There are several options here which will vary in usefulness depending on your situation. We have recommended three below, but there are many other options.
easystats
The easystats ecosystem has lots of different options to suit your needs when it comes to statistics or reporting. For our purposes the report package is a good place to start. When you come to your analysis journey check back with easystats to see if there is a tool to make your life easier in there.
Stargazer
The stargazer package is a tool to make tables from your analysis in a publication ready format. This is a helpful tutorial to get started.
Broom
The broom package is a helper tool designed to tidy up the output you get from statistical models in R. It will convert these to a data frame object which will be easier to work with and present.
Our goal here is the following:
- Use the report library from easystats to make a verbal report on both your regression results! The example below is for the simple linear regression.
We fitted a linear model (estimated using OLS) to predict imd_decile with whr
(formula: imd_decile ~ whr). The model explains a statistically not significant
and very weak proportion of variance (R2 = 3.44e-04, F(1, 2932) = 1.01, p =
0.315, adj. R2 = 3.04e-06). The model's intercept, corresponding to whr = 0, is
at 5.05 (95% CI [4.04, 6.07], t(2932) = 9.80, p < .001). Within this model:
- The effect of whr is statistically non-significant and negative (beta =
-0.61, 95% CI [-1.80, 0.58], t(2932) = -1.00, p = 0.315; Std. beta = -0.02, 95%
CI [-0.05, 0.02])
Standardized parameters were obtained by fitting the model on a standardized
version of the dataset. 95% Confidence Intervals (CIs) and p-values were
computed using a Wald t-distribution approximation.- Use broom to make nice results for your t-test and anova to make it easier to write out your results. Below is an example of our t-test on difference in IMD decile between people who are from Hackney and Westminster.
# A tibble: 1 × 10
estimate estimate1 estimate2 statistic p.value parameter conf.low conf.high
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 -2.77 2.82 5.59 -19.5 3.31e-63 496. -3.05 -2.49
# ℹ 2 more variables: method <chr>, alternative <chr>- Use stargazer to make a nice table for your regression results. The example below is for the simple linear regression.
IMD Decile regression results
===============================================
Dependent variable:
---------------------------
imd_decile
-----------------------------------------------
whr -0.611
(0.608)
Constant 5.055***
(0.516)
-----------------------------------------------
Observations 2,934
R2 0.0003
Adjusted R2 0.00000
Residual Std. Error 2.345 (df = 2932)
F Statistic 1.009 (df = 1; 2932)
===============================================
Note: *p<0.1; **p<0.05; ***p<0.01For stargazer we used type = 'text' to get our output. There are several different outputs formats you can choose.
Other options for making nice outputs for reports
The options we have outlined above are just a few of the many options out there!
One of my favourite packages for presenting descriptive and statistical models in R is the modelsummary package. It can output into multiple formats, depending on how you are writing your reports.
A good option for those who are writing reports that use APA referencing style is the apaTables package. A useful feature is the tables produced can be outputted in multiple different formats such as Word or LaTeX.
If you have some specific output you need then you can write some code yourself to achieve that. For example, say I wanted to make a table of descriptive statistics where the rows of the table are column names and columns are the descriptives (mean, min etc.) I could write some code to do just that.
mean median min max standard_deviation
bmi 23.99 23.39 8.37 54.37 5.74
age 48.24 48.00 16.00 80.00 18.42
imd_decile 4.54 4.00 1.00 10.00 2.34Here is the function I wrote for this example which you are welcome to use and adjust!
Final challenge!
For our last challenge we have provided a few example datasets for you to explore and analyse!
Pick one of the datasets to work with. Can you apply what you have covered so far to a fresh dataset?
We are not going to dictate what you do or how you approach this. We will be available to support you and answer questions.
Some things for you to think about:
What steps do you need to go through to have your data ready for analysis?
What data visualisations can you make, and what would be useful or interesting to look at?
How do you decide what analysis to do?
Wiki temperature data
This dataset is a list, taken from Wikipedia, of the average temperatures of world cities. To get the data, use the code provided below.
The rvest package should have been installed when you installed the tidyverse set of packages. It is used to scrape data from the web using R.
library(rvest)
library(tidyverse)
url <- "https://en.wikipedia.org/wiki/List_of_cities_by_average_temperature"
webpage <- read_html(url)
city_table <- html_nodes(webpage, "table") %>%
html_table(fill = TRUE) %>%
bind_rows() %>%
select(-Ref.) %>%
mutate(across(everything(), function(x) str_remove_all(x, "\\(.*\\)"))) %>%
mutate(across(Jan:Year, function(x) str_replace(x, "−", "-"))) %>%
mutate(across(Jan:Year, as.numeric))UK Gender pay gap data
This data provides information on differences in pay between men and women in the UK. Data is from the Office of National Statistics and was collected from one of their data pages.
Use the code below to load the data.
paygap <- read.csv("https://raw.githubusercontent.com/andrewmoles2/TidyTuesday/master/paygap-2022-06-28/data/paygap.csv")Eurovision song contest
The Eurovision song contest is a music competition that runs every year. Data was collected and made available through this GitHub page.
Use the code below to load the data.
eurovision <- read.csv("https://raw.githubusercontent.com/andrewmoles2/eurovision-contest/main/data/eurovision_data.csv")Pokémon video game data
Pokémon is a card game, TV series, and video game. This dataset is based on the video game. Data has been collected and made available through this GitHub page.
Use the code below to load the datasets.
pokemon_stats <- read.csv("https://raw.githubusercontent.com/andrewmoles2/pokemon-video-games/main/data/pokemon_stats.csv")
pokemon_types <- read.csv("https://raw.githubusercontent.com/andrewmoles2/pokemon-video-games/main/data/pokemon_types.csv")Next steps
If you want to use something other than Microsoft Word to write your reports or dissertation we recommend coming to our Introduction to LaTeX or Report Writing with Markdown workshops. These workshops use a more programmic style for writing reports that gets around the many issues you commonly face using MS Word to write longer documents like a dissertation! If you go for the Report Writing with Markdown workshop we can teach you how to write your analysis and your dissertation in one document for maximum efficiency.
Links to sign up or express interest in the courses are below.
Give us some feedback!
We are always looking to improve and iterate our workshops. Follow the link to give your feedback.
Solutions are available at the end of the survey.